The imitation of the three-dimensional arts of plaiting, weaving and basketry was the origin of interlaced and knotwork interlaced designs. There are few races who have not used it as a decoration of stone, wood and metal. Interlacing rosettes, friezes and ornaments are to be found in the art of most peoples surrounding the Mediterranean, the Black and Caspian Seas, Egyptians, Greeks, Romans, Byzantines, Moors, Persians, Turks, Arabs, Syrians, Hebrews and African tribes. Their highlights are Celtic interlacing knotworks, Islamic layered patterns and Moorish floor and wall decorations.

Their common geometrical construction principle, discovered by P.Gerdes, is the use of (two-sided) mirrors incident to the edges of a square, triangular or hexagonal regular plane tiling, or perpendicular to its edges in their midpoints. In the ideal case, after the series of consecutive reflections, the ray of light reaches its beginning point, defining a single closed curve. In other cases, the result consists of several such curves.

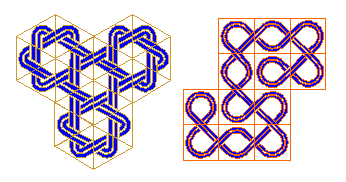
For example, to the Celtic designs from G.Bain book "Celtic Art" correspond the following mirror-schemes:

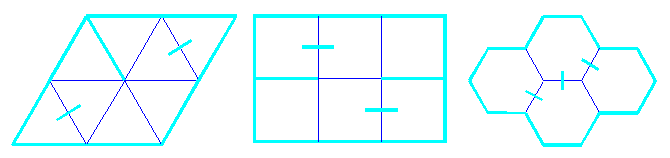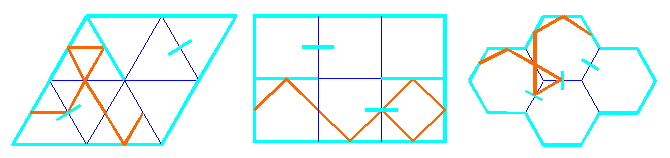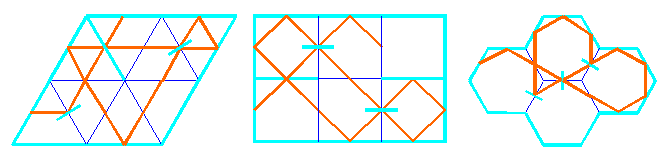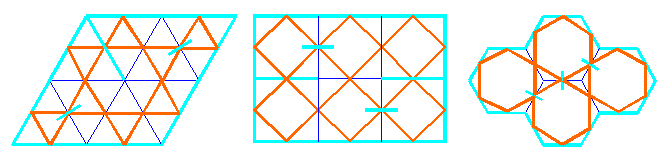
Trying to discover their common mathematical background, they appear two questions: how to construct such a perfect curve - a single line placed uniformly in a regular tiling, this means, how to arrange the set of mirrors generating it, and how to classify the curves obtained. In principle, any polyomino (polyiamond or polyhexe) with mirrors on its border, and two-sided mirrors between cells or perpendicular to the internal cell-edges in their midpoints, could be used for the creation of the corresponding curves.

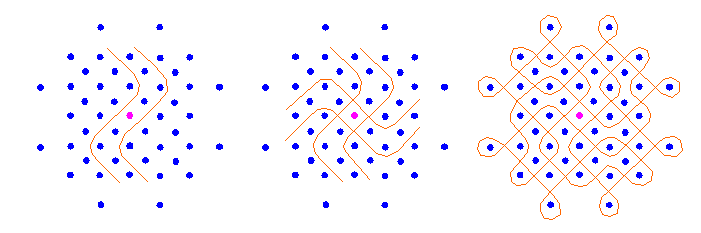
For their construction in some polyomino (polyiamond or polyhexe), we propose the following method. First, we construct all the different curves in it without using internal mirrors, starting from different cell-edge midpoints and ending in them, till the polyomino is exhausted, i.e. uniformly covered by k curves. After that, we may use "curve surgery" in order to obtain a single curve, according to the following rules:

In every polyomino we may introduce k-1, k, k+1,..., 2A-P/2 internal two-sided mirrors, where A is the area and P is the perimeter of the polyomino. Introducing the minimal number of mirrors k-1, we first obtain a single curve, and in the next steps we try to preserve that result.

In the case of a rectangular square grid RG[a,b] with the sides a, b, the initial number of curves, obtained without using internal mirrors is k = gcd(a,b) (greatest common divisor), so in order to obtain a single curve, the possible number of internal two-sided mirrors is k-1, k,..., 2ab-a-b. According to the rules for introduction of internal mirrors, we propose the following algorithm for the production of monolinear designs: in every step, each from the first internal k-1 mirrors must be introduced in crossing points belonging to different curves. After that, when the curves are connected and transformed into a single line, we may introduce other mirrors, taking care about the number of curves, according to the rules mentioned. For example:

The symmetry of such curves is used for the classification of the Celtic frieze designs by P.Cromwel, and for the reconstruction of Tamil designs by P.Gerdes.

From the ornamental heritage, at first glance it looks that the symmetry is the mathematical basis for their construction and possible classification. But, the existence of such asymmetrical curves suggests the other approach.

First criterion that we may use is the geometrical one: two curves are equal iff there is a similarity transforming one into the other. This means, that one curve can be obtained from the other by a combined action of a proportionality and isometry. Instead of considering the curves, we may consider the equal mirror arrangements defined in the same way. Having the algorithm for the construction of such perfect curves and the criterion for their equality, we may try to enumerate them: to find the number of all the different curves (i.e. mirror arrangements) which can be derived from a rectangle with the sides a, b, for a given number of mirrors m (m = k-1, k, ..., 2ab-a-b).

The other point of view to the classification of such perfect curves is that of the knot theory. Every such curve can be simply transformed into an interlacing knotwork design, this means, into the projection of some alternating knot.