|
2. 5/6 fullerenes Among general fullerenes we could distinguish the class
consisting of 5/6 fullerenes with pentagonal or hexagonal faces. If n5
is the number of pentagons, and n6 the number of hexagons,
from the relationship 3v=2e and Euler theorem directly follows
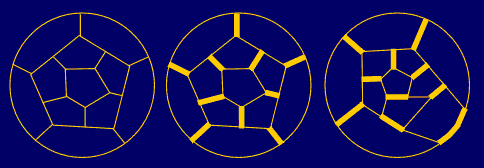
that n5=12, so the first 5/6 fullerene will be C20
with n6=0 – the regular dodecahedron {5,3}, giving possibility
for two non-isomorphic edge-colorings, resulting in two chemically different
isomers of the same geometrical dodecahedral form (Fig.
3). The first basic polyhedra generating 5/6 fullerenes will be that
with v=10 vertices. For v=10, there are three basic polyhedrons,
but only 10* and 10** could generate 5/6 fullerenes,
each only one of them (Fig. 4a).
On the other hand, they generate, respectively, 78 and 288 general fullerenes.
This way, we have two mutually dual methods for the derivation of fullerenes:
(a) edge-coloring of a 3-regular graph, with one colored edge in each vertex;
(b) introduction of a digon in every vertex of 4-regular graph, giving
possibility for a double check of the results obtained. Their duality is
illustrated by the example of two C20 chemical isomers derived,
both of the same geometrical dodecahedral form with G= [3,5]=Ih
=S5 of the order 120, but the
first with G'= D5d=[2+,10]=
D5xC2 of the order 20, and the
other with G'=[2,2]+=D2
of the order 4 (Fig. 3,4a).
In this case, the symmetry of chemical isomers derived by the vertex bifurcation
is preserved from their generating basic polyhedra (Fig.
4a).
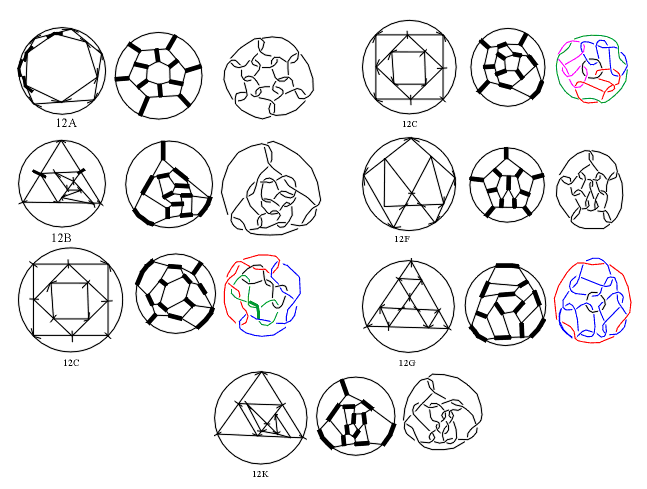
 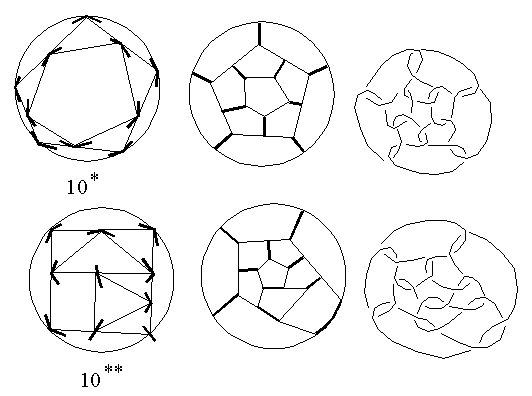 For the enumeration of general fullerenes we used Polya enumeration theorem [6], applied to basic polyhedra knowing their automorphism groups, but with the restriction to 5/6 fullerenes its application is not possible. With the same restriction, the other derivation method: edge-coloring of 3-regular graphs is also not suitable for the application of Polya enumeration theorem, because of the condition that in every vertex only one edge must be colored. The basic polyhedra with n<13 vertices are derived by T.P.Kirkman [1], and used in the works by J.Conway (only for n<12) [2], A.Caudron [3] and S.V.Jablan (for n<13) (Fig. 2) [4]. The 3-connected 4-regular planar graphs (corresponding to basic polyhedra) are enumerated by H.J.Broersma, A.J.W.Duijvestijn and F.Göbel (n<16) [7] and by B.M.Dillencourt (n<13) [8], but given only as numerical results without any data about individual graphs. The 3-regular graphs with n<13 vertices and their edge-colorings producing 4-regular graphs are discussed by A.Yu.Vesnin [9]. Proceeding in the same way, it is possible to prove that
5/6 fullerenes with 22 atoms not exist at all, and that they are seven
5/6 fullerenes C24 of the same geometrical form with G=D6d
=[2+,12]=D12 (Fig.
5). To distinguish different chemical isomers, sometimes even knowing
their chemical symmetry group G' will be not sufficient. For their
exact recognition we could use some results from the knot theory [10]:
the polynomial invariant of knot and link projections, introduced by the
author [11]. Every 4-regular graph
could be transformed into the projection of an alternating knot or link
(and vice versa), and the correspondence between such alternating
knot or link diagrams and 4-regular graphs is 1-1 (up to enantiomorphism)
(Fig. 4b).
 |