|
5. Nanotubes, conical and biconical fullerenes and their symmetry For denoting different categories of symmetry groups, we will use Bohm symbols [16]. In a symbol Gnst…, the first subscript n represents the maximal dimension of space in which the transformations of the symmetry group act, while the following subscripts st… represent the maximal dimensions of subspaces remaining invariant under the action of transformations of the symmetry group, that are properly included in each other. With regard to their symmetry, general fullerenes belong to the category of point groups G30. The category G30 consists of seven polyhedral symmetry groups without invariant planes or lines: [3,3] or Td, [3,3]+ or T, [3,4] or Oh, [3,4]+ or O, [3+,4] or Th, [3,5] or Ih, [3,5]+ or I, and from seven infinite classes of point symmetry groups with the invariant plane (and the line perpendicular to it in the invariant point): [q] or Cqv, [q]+ or Cq, [2+,2q+] or S2q, [2,q+] or Cqh, [2,q]+ or Dq, [2+,2q] or Dqd, [2,q] or Dqh, belonging to the subcategory G320 [5]. For the groups of the subcategory G320, in the case of rotations of order q>2, the invariant line (i.e. the rotation axis) may contain 0,1 or 2 vertices of a general fullerene. According to this, among all general fullerenes with a geometrical symmetry group G belonging to G320, from the topological point of view we could distinguish, respectively, cylindrical fullerenes (nanotubes), conical and biconical ones. We could simply conclude that for polyhedral 5/6 fullerenes
G could be only [3,3] (Td ), [3,3]+
(T), [3,5] (Ih), [3,5]+ (I),
because of their topological structure (n5=12), incompatible
with the octahedral symmetry group [3,4] (Oh) or its
polyhedral subgroups. In the case of nanotubes (or cylindrical fullerenes)
we have infinite classes of 5/6 fullerenes with the geometrical symmetry
group [2,q] (Dqh) and [2+,2q]
(Dqd), and the same chemical symmetry. The first infinite
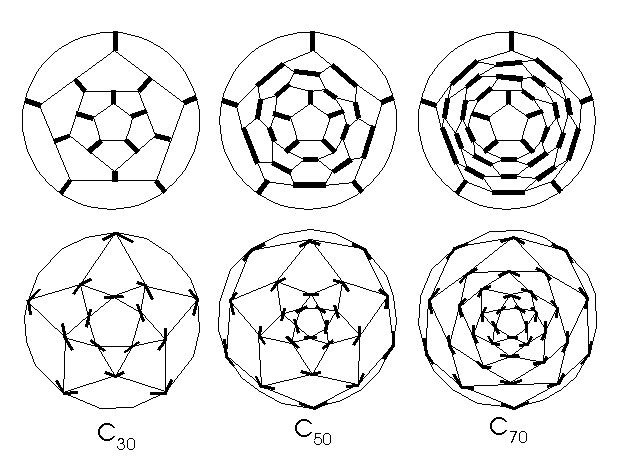
first class of cylindrical nanotubes with G=G'=D5h
we obtain from a cylindrical 3/4/5 4-regular graph with two pentagonal
bases, 10 triangular and 5(2k+1) quadrilateral faces (k=0,1,2,…)
and with the same symmetry group (Fig.
11). By the vertex bifurcation preserving its symmetry, we obtain the
infinite class of nanotubes C30, C50, C70,…,
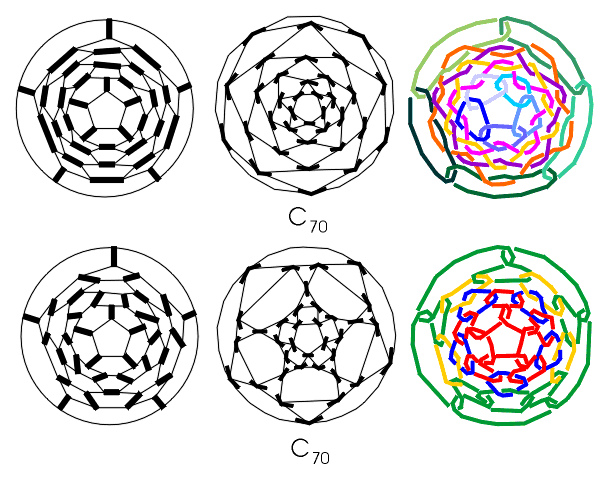
with C70 as the first of them satisfying IPR. Certainly, the
geometrical structure of C70 admits different edge colorings
(i.e. chemical isomers). Starting from any two of them (Fig.
12) by "collapsing" (the inverse of "vertex bifurcation", i.e. by deleting
digons) we could obtain different generating 4-regular graphs. This example
of two different C70 isomers, with the same geometrical structure,
and with the same G and G', shows that for the exact recognition
of fullerene isomers we need to know more than their geometrical and chemical
symmetry (see Part 3). In the same way, from 4-regular graphs with two
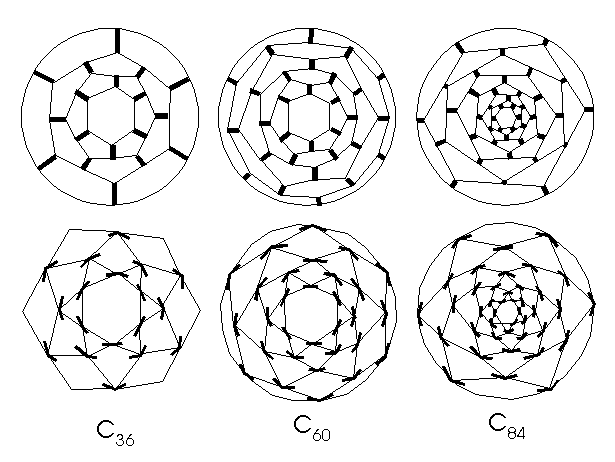
hexagonal bases, 12 triangular and 6(2k+1) quadrilateral faces (k=0,1,2,…)
we obtain the infinite class of fullerenes C36, C60
C84,… with the symmetry group G=G'=D6h
(Fig. 13).
   The next symmetry groups [2+,2q] (Dqd)
with q=5,6 we obtain in the same way, from 4-regular graphs with
q-gonal bases, 2q triangular and 2kq quadrilateral
faces (k=1,2,… for q=5; k=0,1,2,… for q=6)
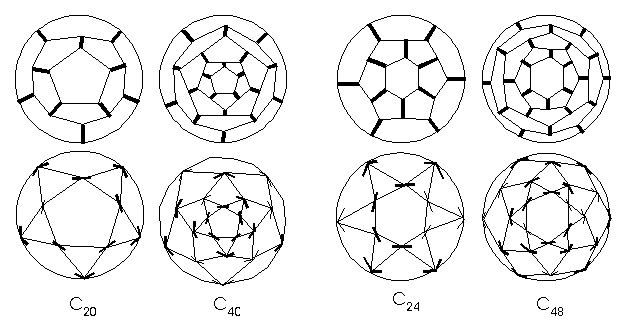
(Fig. 14). As the limiting case,
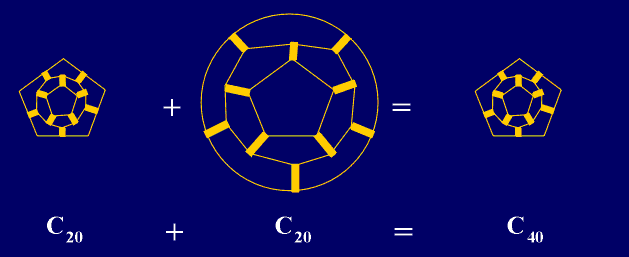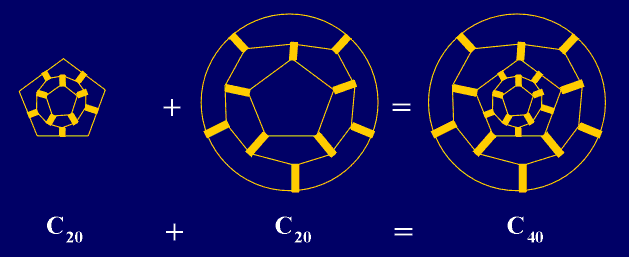
for q=5 and k=0, we obtain C20 with the icosahedral
symmetry group G, but with G'=D5d,
that could be used as the "brick" for the complete class of nanotubes C40,
C60,C80,… with G= D5d,
where all of them could be obtained from C20 by "gluing" the
pentagonal bases (Fig. 15). In
the same way, fullerene C24 obtained for q=6 and k=0
could be used as the building block for the nanotubes C48, C72,C96,…
The geometrical structure of nanotube class with G=Dqd
(q=5,6) permits the edge coloring preserving the symmetry, so there
always exist their isomers with G=G'.
  If the 3-rotation axis contains the opposite vertices
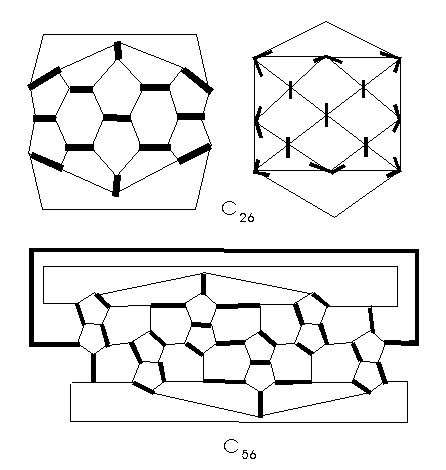
of a fullerene, we have biconical fullerenes (e.g. C26, C56)
with G=D3h, G=D3d,
respectively (Fig. 16). Certainly,
after the edge coloring, their symmetry must be disturbed, and for them
G' is always a proper subgroup of G. For example, for C26
(Fig. 16), G=D3h,
G'=C2v.
 Proceeding in the same way, it is possible to find or
construct fullerene representatives of other symmetry groups from the category
G320: biconical C32 with G=D3,
biconical C38 or conical C34 with G=C3v,
conical C46 with G=C3 [17],
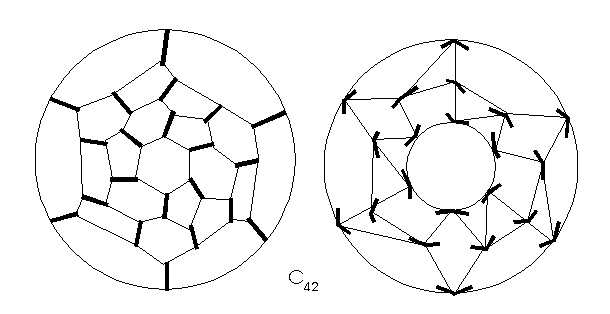
or the infinite class of cylindrical fullerenes C42, C48,
C54… with G=D3 (Fig.
17). In general, after edge coloring of their 3-regular graphs, symmetry
could not be preserved in all conical or biconical fullerenes mentioned,
so their geometrical symmetry is always higher than the chemical.
 |