Using the mentioned connection between alternating knot or link diagrams and 4-regular (chemical) Schlegel diagrams of fullerenes, it is interesting to consider all of them after such conversion. For example, two chemical isomers of C₂₀ will result in knots, and from 7 isomers of C₂₄ we obtain four knots, one 3-component, one 4-component and one 5-component link. 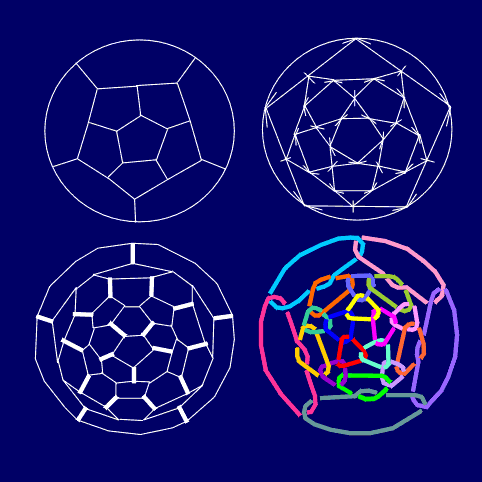Among the links obtained, two of them (3-component and 5-component one) contain a minimal possible component: hexagonal carbon ring (or simply, a circle). It is interesting that C₆₀ consists only of such regularly arranged carbon rings, so maybe this could be another additional reason for its stability (Fig. 7). Therefore, it will be interesting to consider the infinite class of 5/6 fullerenes with that property, that will be called "perfect". Some of "perfect" fullerenes are modeled with hexastrips by P.Gerdes [13], and similar structures: buckling patterns of shells and spherical honeycomb structures are considered by different authors (e.g. T.Tarnai [14]).
  

 

To obtain them, we will start from some 5/6 fullerene given in geometrical form (i.e. by a 3-regular graph). Than we could use "mid-edge-truncation" and vertex bifurcation in all vertices of the triangular faces obtained that way, transforming them into hexagons with alternating digonal edges. Let is given some fullerene (e.g. C₂₀) in its geometrical form (i.e. as 3-regular graph). By connecting the midpoints of all adjacent edges we obtain from it the 3/5 fullerene covered by connected triangular net and pentagonal faces preserved from C₂₀. After that, in all the vertices of the truncated polyhedron we introduce digons, to transform all triangles into hexagonal faces. This way, from C₂₀ we derived C₆₀ (in its chemical form) (Fig. 7). The mid-edge-truncation we could apply to any 5/6 (geometrical) fullerene, to obtain new "perfect" (chemical) fullerene, formed by carbon rings. This way, from a 5/6 fullerene with v vertices we always may derive new "perfect" 5/6 fullerene with 3v vertices (Fig. 8). Moreover, the symmetry of new fullerene is preserved from its generating fullerene. According to the theorem by Grünbaum & Motzkin [15], for every non-negative n₆ unequal to 1, there exists 3-valent convex polyhedron having n₆ hexagonal faces. Hence, from the infinite class of 3-regular 5/6 polyhedra with v=20+n₆ vertices, we obtain the infinite class of "perfect" fullerenes with v=60+3n₆ vertices. The "perfect" fullerenes satisfy two important chemical conditions: (a) the isolated pentagon rule (IPR); (b) hollow pentagon rule (HPR). The IPR rule means that there are no adjacent pentagons, and HPR means that all the pentagons are "holes", i.e. that every pentagon could have only external double bonds. The first 5/6 fullerene satisfying IPR is C₆₀, and it also satisfies HPR. The IPR is well known as the stability criterion: all fullerenes of lower order (less than 60) are unstable, because they don't satisfy IPR. On the other hand, C₇₀ satisfies IPR, but cannot satisfy HPR (Fig. 9).
  

 

 

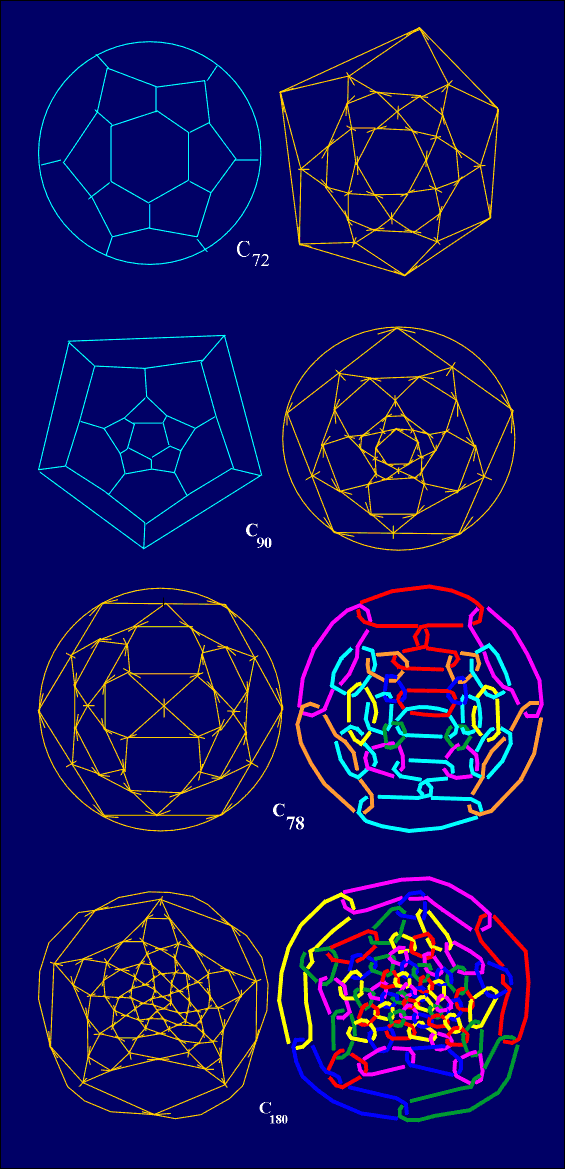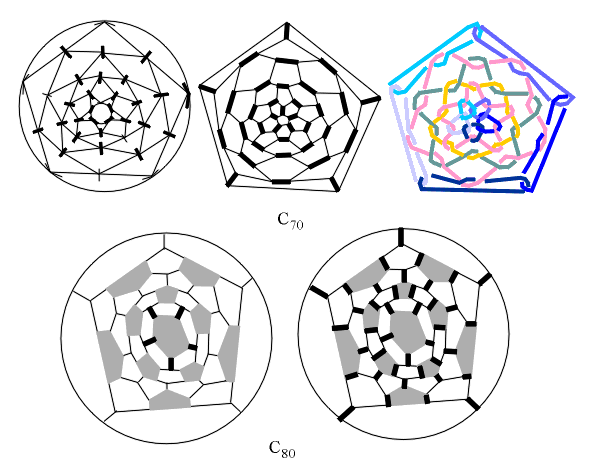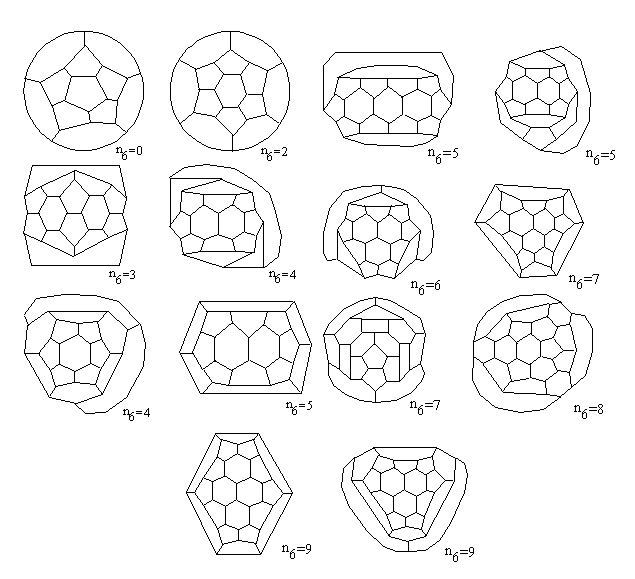
The same situation is with C₈₀, possessing the same icosahedral geometrical symmetry as C₆₀, but not able to preserve it after edge-coloring, because HPR cannot be satisfied (Fig. 9). This is the reason that only "perfect" fullerenes, with G=G'= [3,5]=I_h=S₅, satisfying both IPR and HPR will be C₆₀, C₁₈₀, C₂₄₀, etc. We need also to notice that for n₆= 0,2,3 we have always one 3-regular 5/6 polyhedron (i.e. geometrical form of C₂₀, C₂₄, C₂₆), but for some larger values (e.g. n₆= 4,5,7,9) there are several geometrical isomers of the generating fullerene, and consequently, the same number of "perfect" fullerenes derived from them (Fig. 10). Hence, considering the fullerene isomers, we could distinguish "geometrical isomers", this means, different geometrical forms of some fullerene treated as 3-regular 5/6 polyhedron, and "chemical isomers" – different arrangements of double bonds, obtained from the same 3-regular graph by its edge-coloring.