From the tetravalence of C result four possible vertex situations, that could be denoted as 31, 22, 211 and 1111 (Fig. 1a). The situation 31 could be obtained by adding two C atoms between any two others connected by a single bond, and situation 22 by adding a C atom between any two others connected by a double bond (Fig. 1b). Therefore, we could restrict our consideration to the remaining two non-trivial cases: 211 and 1111. Working in opposite sense, we could always delete 31 or 22 vertices, and obtain a reduced 4-regular graph, where in each vertex occurs at most one double bond (digon), that could be denoted by colored (bold) edge (Fig. 1a). First, we could consider all 4-regular graphs on a sphere, from which non-trivial in the sense of derivation are only reduced ones. In the knot theory, 4-regular graphs on a sphere with all vertices of the type 1111 are known as "basic polyhedra" [1,2, 3,4], and that with at least one vertex with a digon as "generating knots or links" [4]. From the chemical reasons, the vertices of the type 1111 are only theoretically acceptable. If all the vertices of such 4-regular graph are of the type 211, such graph we will be called a general fullerene. Every general fullerene could be derived from a basic polyhedron by "vertex bifurcation", this means, by replacing its vertices by digons, where for their position we have always two possibilities (Fig. 1c). To every general fullerene corresponds (up to isomorphism) an edge-colored 3-regular graph (with bold edges denoting digons). This way, we have two complementary ways for the derivation of general fullerenes: vertex bifurcation method applied to basic polyhedra, or edge-coloring method applied to 3-regular graphs, where in each vertex there is exactly one colored edge. For every general fullerene we could define its geometrical structure (i.e. the positions of C atoms) described by a non-colored 3-regular graph, and its chemical structure (i.e. positions of C atoms and their double bonds) described by the corresponding edge-colored 3-regular graph. In the same sense, for every general fullerene we could distinguish two possible symmetry groups: a symmetry group G corresponding to the geometrical structure and its subgroup G' corresponding to the chemical structure. In the same sense, we will distinguish geometrical and chemical isomers. For example, for C₆₀, G=G'=[3,5]=I_h =S₅ of order 120 [5], but for C₈₀ with the same G, G' is always a proper subgroup of G, and its chemical symmetry is lower than the geometrical. Hence, after C₆₀, the first fullerene with G=G'= [3,5]=I_h=S₅ will be C₁₈₀, then C₂₄₀, etc.
  

 

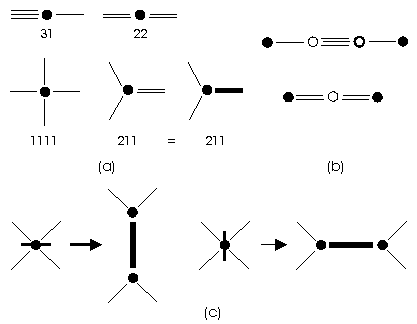Working with general fullerenes without any restriction for the number of edges of their faces, the first basic polyhedron from which we could derive them (after the trivial 1*) will be the regular octahedron {3,4} or 6^*, from which we obtain 7 general fullerenes. From the basic polyhedron 8^* with v=8 we derive 30, and from the basic polyhedron 9^* we obtain 4 general fullerenes. All the basic polyhedra with v<13 and their Schlegel diagrams are given by Fig. 2.
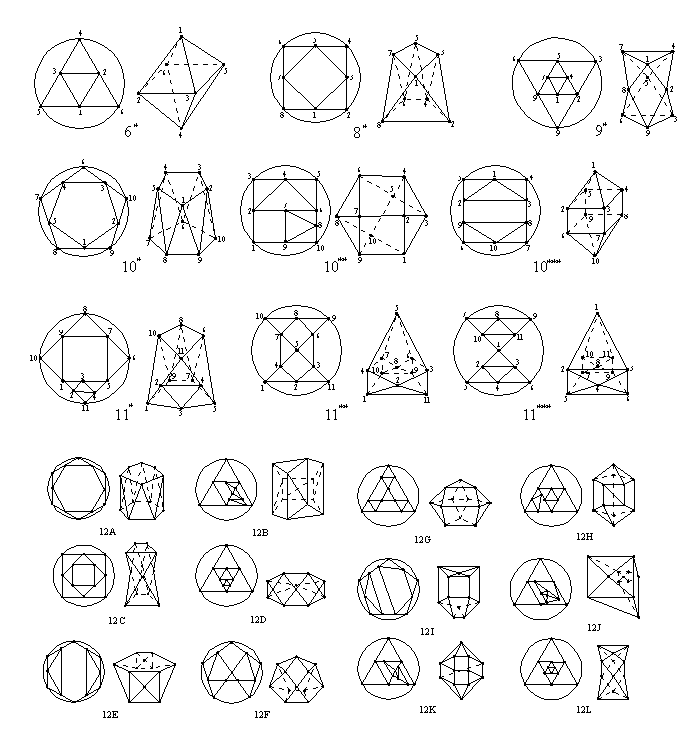