Let be given an oriented knot or link diagram D with generators g₁,…, g_n [12]. If the generators g_i, g_j, g_k are related as in Fig. 6a, then a_ii= -t, a_ij= 1, a_ik= -1; if they are related as in Fig. 6b, then a_ii= t, a_ij= 1, a_ik= -1; in all the other cases a_ij=0. The determinant d(t)=|a_ij| is the polynomial invariant of D. In the case of links, in this polynomial invariant we use for generators of different components different variables (up to a permutation of variables). For example, let us show that two isomers of C₂₀ are different (Fig. 3-4, 6c). After converting their chemical Schlegel diagrams into the alternating knot diagrams, denoting their generators, and calculating the corresponding determinants we obtain, respectively, D₁=t²⁰ -10t¹⁸+45t¹⁶-120t¹⁴ +200t¹²-197 t¹⁰ +105t⁸-40t⁶+25t⁴ -10t² and D₂=t²⁰ -10t¹⁸+45t¹⁶-120t¹⁴ +208t¹²-250t¹⁰ +217t⁸-130t⁶+49t⁴ -10t², proving their difference. On the other hand, for three-component alternating links corresponding to the diagrams (Fig. 6d), using the same multivariable invariant for link projections, we conclude that they both represent the isomorphic Schlegel diagrams of the same fullerene C₂₄.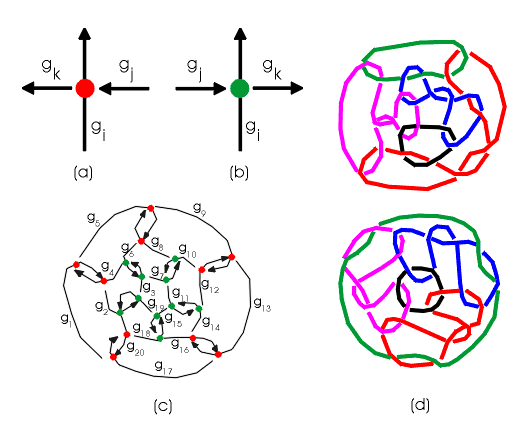